Ces expériences de physique amusante sont faciles à réaliser. Attention, ne jamais regarder directement le soleil ! Il est nécessaire de faire l’expérience un jour bien ensoleillé. Il est nécessaire d’avoir lu l’article Voir l’image du soleil pour comprendre l’expérience présentée ici.
Matériel
- une feuille de papier petits carreaux (de préférence)
- un mètre ruban
- un grand carton (qui servira d’écran)
- un carton (type couvercle de carton de chaussures)
- un clou de diamètre 1ou 2 mm
Protocole
Conformément à l’article Voir l’image du soleil, on va réaliser un dispositif expérimental permettant de voir l’image du soleil. Pour ce faire, scotcher du papier petits carreaux sur un grand carton et placer ce dernier près du sol. Placer un objet sous le carton et incliner ce dernier de sorte que le plan du carton soit perpendiculaire approximativement à l’axe (soleil/carton). Ce grand carton jouera le rôle d’écran.
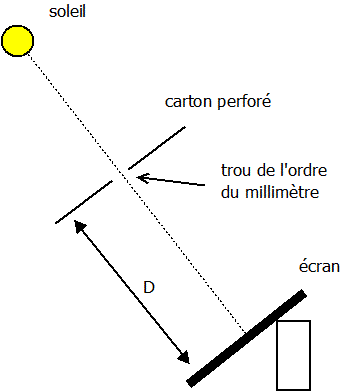
(D est de l’ordre du mètre)
Créer un trou de l’ordre du millimètre (à l’aide d’un clou par exemple) dans un petit carton puis l’éloigner de l’écran d’au moins une distance de un mètre.



Observer sur l’écran l’image alors formée. Vous pouvez étudier l’influence de la distance D entre le trou et l’écran sur la forme de l’image ainsi que l’influence de la perpendicularité de plan de l’écran avec l’axe soleil/trou.
Pour une configuration donnée de l’expérience, observer également l’évolution de l’image du soleil en fonction du temps (on peut faire les observations sur une quinzaine de minutes).
Observations
Si l’écran est bien perpendiculaire à l’axe soleil-trou, l’image observée est circulaire et uniformément éclairée (sauf bien sûr en cas d’éclipse solaire ou de passage de nuages…). L’image formée peut avoir une forme elliptique si la perpendicularité n’est pas assurée.

SI la distance reste suffisamment grande devant la taille du trou, on peut constater que la taille de l’image augmente lorsque la distance D augmente. Enfin, l’image observée se déplace au cours du temps sur l’écran.
Interprétation
L’image formée sur l’écran est celle du soleil : plus précisément, il s’agit d’une image inversée du soleil ! Le dispositif précédent fonctionne comme un sténopé ou encore comme une chambre noire (voir dessin ci-dessous).
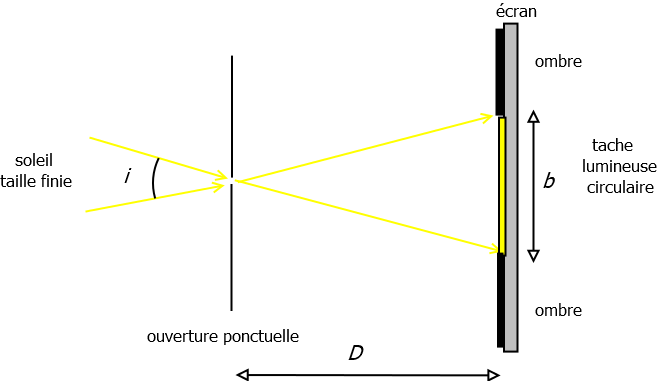
Dans l’article Voir l’image du soleil, nous avons déjà étudié l’influence de la distance D sur la forme de l’image. Dans le cas de la configuration « sténopé », grâce au dessin précédent, nous comprenons bien pourquoi la taille de l’image augmente lorsque la distance D augmente, la taille de la tache lumineuse sur l’écran étant proportionnelle à la distance D. Il est facile de comprendre également pourquoi l’image est circulaire si la perpendicularité soleil-trou est assurée et de forme elliptique sinon.
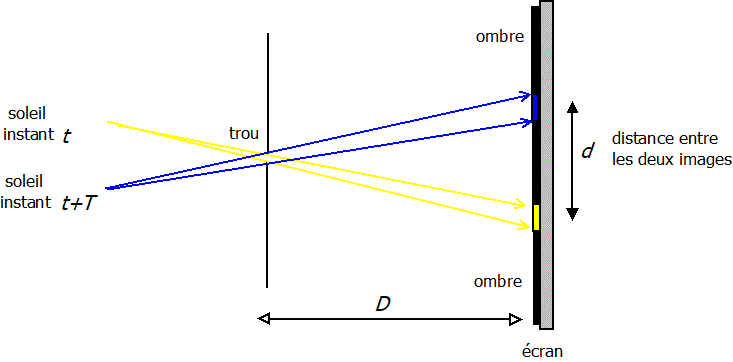
Enfin, au cours de la journée, lorsque le soleil « tourne », l’image formée se déplace également sur l’écran. Ce constat se comprend également très facilement à l’aide du dessin ci-dessus.
Quelques mesures

Dans un premier temps, nous vous proposons de mesurer la taille du soleil !
Pour ce faire, mesurer la distance D entre l’ouverture réalisée dans le carton et l’écran. Puis mesurer le diamètre b de l’image de soleil sur l’écran. A partir de ces deux mesures, vous pouvez en déduire le diamètre angulaire du soleil : i = b / D en radians. Connaissant la distance qui sépare la Terre du soleil (L=150 millions de km), on peut mesurer facilement la taille du soleil ! Il suffit de multiplier l’angle i (en radians) par L (il s’agit encore pour ceux qui connaissent d’appliquer un théorème de Thalès). Alors, que trouvez-vous ?
Dans un second temps, nous vous proposons de mesurer la vitesse angulaire de rotation de la Terre autour d’elle même. A un instant donné, à l’aide d’une croix tracée avec un stylo, repérer où se trouve l’image du soleil sur l’écran. Réaliser le même relevé T = quinze minutes plus tard. Mesurer la distance d entre les deux positions précédente. Vous pouvez en déduire la vitesse angulaire de rotation de la terre autour d’elle même en effectuant le rapport d / (D.T). Vous pouvez vérifier bien sûr ensuite si cette valeur correspond bien à la valeur connue de un tour par 24h (en se souvenant que 1 tour = 360 degrés = 6,28 radians) !